Phi ( = 1.618033988749895... ), most often pronounced fi like "fly," is simply an irrational number like pi ( p = 3.14159265358979... ), but one with many unusual mathematical properties.  Unlike pi, which is a transcendental number, phi is the solution to a quadratic equation.

Phi is the basis for the Golden Section, Ratio or Mean

The ratio, or proportion, determined by Phi (1.618 ...) was known to the Greeks as the "dividing a line in the extreme and mean ratio" and to Renaissance artists as the "Divine Proportion"  It is also called the Golden Section, Golden Ratio and the Golden Mean.

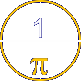Phi, like Pi, is a ratio defined by a geometric construction

Just as pi (p) is the ratio of the circumference of a circle to its diameter, phi () is simply the ratio of the line segments that result when a line is divided in one very special and unique way.

Divide a line so that:

the ratio of the length of the entire line (A)
to the length of larger line segment (B)

is the same as

the ratio of the length of the larger line segment (B)
to the length of the smaller line segment (C).
　

This happens only at the point where:

A is 1.618 ... times B and B is 1.618 ... times C.

Alternatively, C is 0.618... of B and B is 0.618... of A.

Phi with an upper case "P" is 1.618 0339 887 ..., while phi with a lower case "p" is 0.6180339887, the reciprocal of Phi and also Phi minus 1.

DNA in the cell appears as a double-stranded helix referred to as B-DNA. This form of DNA has a two groove in its spirals, with a ratio of phi in the proportion of the major groove to the minor groove, or roughly 21 angstroms to 13 angstroms. 　 HOME